Why simplify terrain and forest?
Modelling in 3D creates a tremendous amount of data. Maintaining and using large datasets presents a challenge. As long as the data that is represented by a 3D model is of added value overcoming these challenges are not a problem. When creating terrain models the algorithm uses Triangulated Irregular Networks (TIN). This is a collection of connected 3D triangles that form a closed surface. The amount of triangles, and therefore vertices, is key in the total storage size of a terrain model.
As described in What does it do? Terrain and Forest class get added additional height points during the reconstruction. These points are the height points that are read from the point files. If the algorithm would add all points the resulting density would be extremely high while the added value would be low for the height information. The software contains several options to filter these additional points. These options are described in the lifting options for Terrain and Forest. The simple version is random simplification opposed to TIN simplification that is a smart error minimisation algorithm.
Random simplification
When configured to use random simplification the algorithm uses a random number generator to decide if a point is used or not. Random filtering using a uniform integer distribution between 1 and configured simplification value. A value of 6 generated equal changes compared to throwing a 6-sided dice.
It is not advised to use this random simplification for production stage. It creates a different outcome each run and does not create a model that describes the terrain in the best way possible. For testing and research purposes this filtering works a lot faster.
TIN simplification
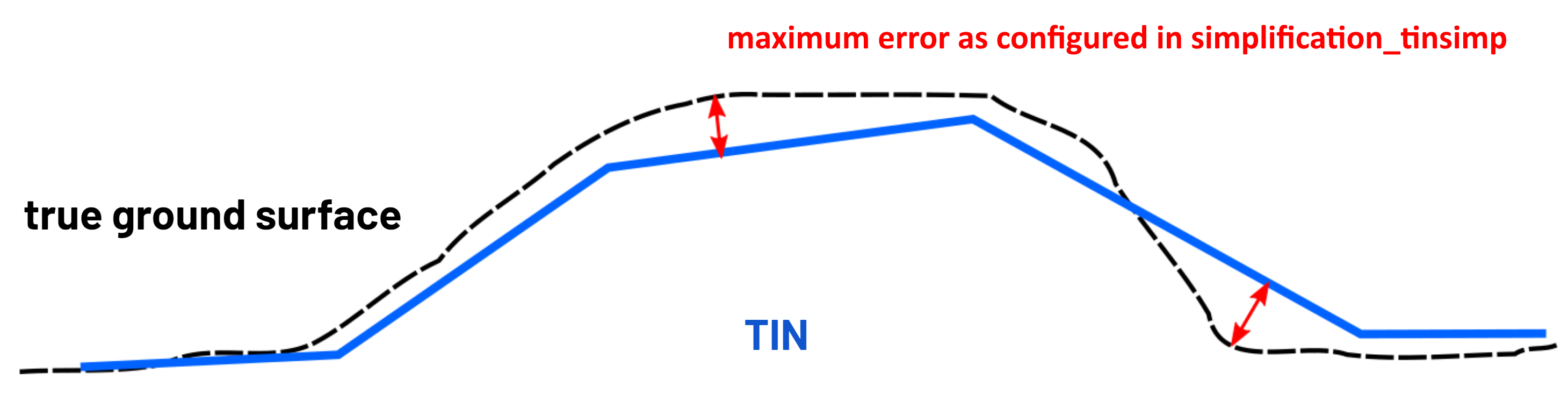
A more robust algorithm for simplification of terrain and forest classes is implemented. It minimises the amount of triangles while it makes sure the set maximum error is not exceeded. Points that do not add more detail to the terrain when added are not used. The minimum detail it needs to add must be higher then the configured simplification distance. The algorithm is based on the paper of Heckbert, P. S., & Garland, M. (1997). Survey of polygonal surface simplification algorithms. It uses Greedy Insertion to add points in a specific order to the triangle mesh so the point with the largest impact on the terrain is processed first. The points are added iteratively up-to the point the calculated error is less then the configured threshold.
In the image the black dashed line called true ground surface is the surface described by the point clouds. The error defined by the TIN and the point cloud is the smallest distance from the point to the TIN.
In the example below there are three cases that show the impact of the simplification_tinsimp setting. On the left is an example of using all points for the Terrain without simplification. The middle permits a maximum error of 5 centimeter (simplification_tinsimp: 0.05) and the right a maximum error of 15 centimeter (simplification_tinsimp: 0.15).

